필자는 Tree 구조에 대해 많이 들었지만 정확히 이해를 하지 못한것 같다.
이번에는 제대로 개념에 대해 이해하고 이것을 코드로도 작성해볼 것이다.
이 글은 다음 사이트들를 참조했다.
출처 사이트 목록 클릭
https://en.wikipedia.org/wiki/Binary_tree
https://yoongrammer.tistory.com/71
https://www.programiz.com/dsa/trees
https://www.geeksforgeeks.org/introduction-to-tree-data-structure/
https://justin-miguel-fernandez.medium.com/algorithm-time-complexity-9bf96bc84d2d
https://www.geeksforgeeks.org/binary-search-tree-data-structure/
1. Tree 데이터 구조란?
트리는 edge에 의해 이어진 노드들로 구성된 비정형 계층형 데이터 구조

2. 왜 Tree Data Structure인가?
다른 데이터 구조(arrays, linked list나 queue) 는 데이터를 연속적으로 저장하는 선형 데이터 구조이다.
선형 데이터 구조에서 어떤 작업을 수행하면 데이터 사이즈의 증가와 마찬가지로 시간 복잡도가 증가한다.
트리 데이터 구조는 데이터 구조가 비선형 데이터 구조일 때 더 빠르고 더 쉬운 접근에 좋다.
3. 용어 정리
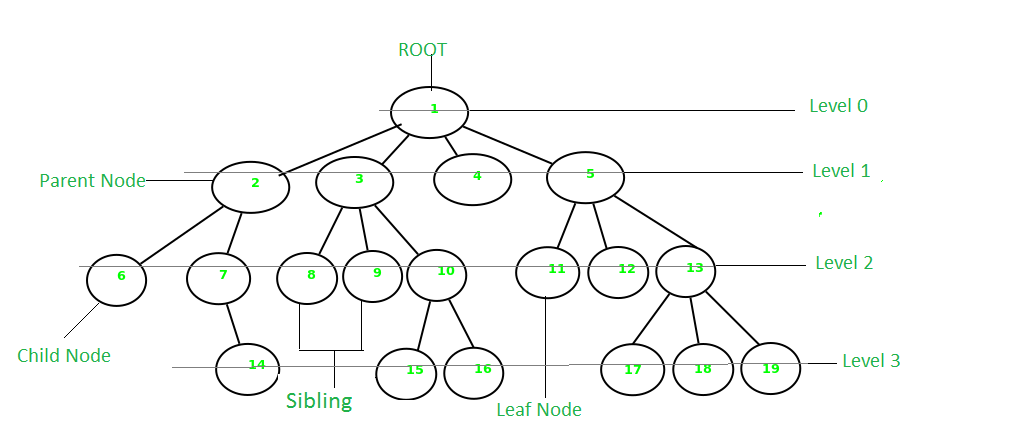
노드 관련 용어 정리 클릭!
- 부모 노드(Parent Node) : 한 노드의 전임자(predecessor)인 노드를 그 노드의 부모 노드라고 한다. 위 그림에서는 level 1에 있는 노드 중 2번이 6,7의 부모 노드이다.
- 자식 노드(Child Node) : 한 노드의 직접적인 후임자(successor)인 노드를 그 노드의 자식 노드라고 한다. level 2에 있는 노드 중 6,7이 level 1 노드중 2의 자식이다.
- 뿌리 노드(Root Node) : 어떤 부모 노드도 가지지 않은 한 tree의 꼭대기 노드를 뿌리 노드라고 한다. level0의 1 노드가 이에 해당한다. 빈 트리가 아니면 반드시 뿌리 노드가 존재한다.
- 노드의 차수(Degree of Node) : 노드에 붙은 하부 트리의 총 갯수를 노드의 차수라고 한다. leaf 노드의 차수는 0이어 한다. tree의 차수는 tree의 모든 노드들 사이에 노드의 최대 차수이다. 노드 3의 차수는 3이다. 즉, 하부 트리의 총 갯수가 3개라는 것이다.
- 리프 노드(Leaf Node) 혹은 (외부 노드) External Node : 자식 노드가 없는 노드들을 리프 노드라고 한다. (나무의 잎사귀처럼 그들이 나무의 마지막임). 6, 14, 8, 9, 15, 16, 4, 11, 12, 17, 18, 19가 이에 해당한다.
- 조상 노드(Ancestor of Node) : 노드의 뿌리의 경로에 전임자 노드들을 조상 노드라고 한다. 예로, 1,2가 7의 조상 노드이다.
- 자손(Descendant) : 리프노드에서 한 노드까지 경로에 후임자 노드. 7, 14 노드가 2 노드의 자손이다.
- 형제(Siblings) : 같은 부모 노드의 자손들을 형제 노드라고 한다. 8, 9, 10는 형제 노드들이다.
- 노드의 깊이(Depth of Node) : 뿌리 노드부터 한 노드의 마지막까지의 갯수를 노드의 깊이라 한다. 노드 14의 깊이는 깊이가 3이다. (뿌리 노드는 0번째부터 시작한다.)
- 노드의 높이(Height of Node) : 한 노드에서 리프 노드까지 가잔 긴 경로를 가진 끝부분들의 갯수를 노드의 높이라고 한다. 노드 3의 높이는 2이다. (노드 3 -> 노드 10 -> 노드 15,16 까지 최대 길이는 높이가 2이다. 노드 3에서 본 자신의 높이는 0이다.)
- 트리의 높이(Height of Tree) : 트리의 높이는 뿌리 노드의 높이다. 즉, 뿌리에서 가장 깊은 노드까지 끝부분의 갯수이다. 위 트리의 높이는 3이다.
- 노드의 레벨(Level of Node) : 뿌리 노드에서 한 노드까지 끝부분들의 갯수. 루트 노드는 레벨이 0이다.
- 내부 노드(Internal node) : 적어도 하나의 자식을 가진 노드를 내부 노드라고 한다.
- 노드의 이웃(Neighbour of a Node) : 한 노드의 부모 혹은 자식 노드를 그 노드의 이웃 노드라고 한다.
- 하부 트리(Subtree) : 그 자손과 함께 있는 트리의 노드.
4. 트리 데이터 구조의 종류
트리 데이터 구조로는 총 4개의 종류가 있다. 일반트리, 이진트리, 평행트리, 이진 탐색트리가 이에 해당한다.
(1) 일반 트리(General tree)
일반 트리 데이터 구조는 노드의 갯수에 제한이 없는 트리. 부모 노드가 자식 노드의 갯수를 제한 없이 가질 수 있다는 말이다.
(2) 이진 트리(Binary tree)
이진트리란 한 노드의 자식 노드가 최대 2개(왼쪽, 오른쪽)인 트리. 다르게 이야기하면, 이진 트리의 노드는 최대 두개의 자식 노드를 가질 수 있다. 정렬이 안되있고, 평형을 이루지도 않았다.
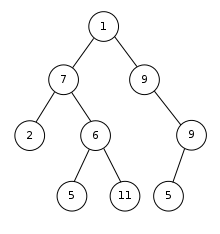
(3) 평형 트리(Balanced tree)
높이가 노드 개수의 대수에 거의 같은 것처럼 치우침이 적은 트리. 특히, 모든 노드에 관해서 좌우의 부분 트리가 같은 정도의 규모가 되도록 균형을 가지게 하고, 탐색이 빨라지도록 준 최적화한 이분 탐색 트리를 가리키는 경우가 많다.


- 왼쪽과 오른쪽 하부 트리 사이의 노드 차이가 하나보다 크면 안된다.
- 왼쪽 하위 트리는 평형이다.
- 오른쪽 하위 트리는 평형이다.
(4) 이진 탐색 트리(General tree)

이진 탐색 트리는 정렬된 이진트리로써 다음과 같은 속성을 가지고 있다.
- 한 노드의 왼쪽 하부 트리는 오직 그 노드의 키보다 더 적은 키들의 노드를 가진다.
- 한 노드의 오른쪽 하부 트리는 오직 그 노드의 키보다 더 큰 키들의 노드를 가진다.
- 왼쪽 오른쪽 하부 트리 각각은 또한 이진 탐색 트리여야만 한다.
여기서 키라고 하면 노드 내부의 값으로 이해하면 된다.

5. 트리 순회(Tree Traversal)
트리를 순회하는 방식으로 3가지를 알아 볼 것이다. 전위 순회, 중위 순회, 후위 순회가 이에 해당한다.
전위 순회는 [루트 - 왼쪽 자식 - 오른쪽 자식] 순으로 순회한다.
중위 순회는 [왼쪽 자식 - 루트 - 오른쪽 자식] 순으로 순회한다.
후위 순회는 [왼쪽 자식 - 오른쪽 자식 - 루트] 순으로 순회한다.
다음에 온 그림을 토대로 순서대로 어떻게 순회하는지 알아보겠다.

(1) 전위 순회 (Preorder Traversal)
루트 노드부터 먼저 방문을 한다. 그리고 왼쪽 서브 트리를 전위 순회한다. 그 다음으로 오른쪽 서브 트리를 전위 순회한다. 즉 노드를 먼저 방문하고 왼쪽 끝까지 내려간 다음 오른쪽으로 이동하여 다시 시작하거나 오른쪽으로 이동하여 순회를 계속하게 된다.
순서대로 한 번 따라가 보겠다.
맨 처음으로 위에서 트리를 전위 순회하려고 한다.
현재 트리의 루트 노드는 맨 위에 있는 F이다.
그리고 왼쪽의 서브 트리인 B로 먼저 들어간다. 왼쪽 자식이 있으니 A로 이동한다. 없으면 나와서 B로 돌아가서 오른쪽 자식을 순회한다.
오른쪽 자식인 D에 왔는데 왼쪽 자식이 있다. C를 순회하고 오른쪽 자식인 E를 순회한다.
그러면 전부 순회했으니 루트 노드의 오른쪽 자식을 순회할 차례다. 같은 방식이 이어진다. 최종 순회 순서는 다음과 같다.
순서 : F -> B -> A -> D -> C -> E ->G -> I -> H
(2) 중위 순회(Inorder Traversal)
왼쪽 서브트리를 후위순회한다. 오른쪽 서브트리를 후위 순회한다. 그 다음에 노드를 방문한다.
왼쪽 끝까지 내려간 이후 노드를 방문하고 오른쪽 자식 노드로 이동하여 순회를 계속 한다.
순서 : A-> B -> C -> D -> E-> F ->G -> H -> I
(3) 후위 순회(Postorder Traversal)
왼쪽 서브트리를 후위순회한다. 오른쪽 서브트리를 후위순회한다. 그리고 노드를 방문한다.
순서 : A-> C-> E -> D -> B-> H -> I -> G -> F
6. 예시
BinaryTree.java
public class BinaryTree {
// Root of Binary Tree
Node root;
BinaryTree() {
root = null;
}
void postorder(Node node) {
if (node == null)
return;
// Traverse left
postorder(node.left);
// Traverse right
postorder(node.right);
// Traverse root
System.out.print(node.item + "->");
}
void inorder(Node node) {
if (node == null)
return;
// Traverse left
inorder(node.left);
// Traverse root
System.out.print(node.item + "->");
// Traverse right
inorder(node.right);
}
void preorder(Node node) {
if (node == null)
return;
// Traverse root
System.out.print(node.item + "->");
// Traverse left
preorder(node.left);
// Traverse right
preorder(node.right);
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(12);
tree.root.right = new Node(9);
tree.root.left.left = new Node(5);
tree.root.left.right = new Node(6);
System.out.println("Inorder traversal");
tree.inorder(tree.root);
System.out.println("\nPreorder traversal ");
tree.preorder(tree.root);
System.out.println("\nPostorder traversal");
tree.postorder(tree.root);
}
}
class Node {
int item;
Node left, right;
public Node(int key) {
item = key;
left = right = null;
}
}
출력 결과 확인 클릭!
Inorder traversal
5->12->6->1->9->
Preorder traversal
1->12->5->6->9->
Postorder traversal
5->6->12->9->1->
Process finished with exit code 0
이번 시간에는 Tree에 대해 좀 알아보았다.
다음에는 이진 트리의 종류에 대해 더 알아보도록 하겠다.
'programming language > Java' 카테고리의 다른 글
| [Java] 배열 - Arrays 정리하기 : 2탄 - copyOfRange, equals, fill, deepEquals (0) | 2023.02.09 |
|---|---|
| [Java] 배열 - Arrays 정리하기 : 1탄 - copyOf, asList, binarySearch (0) | 2023.02.09 |
| Set이란? HashSet, TreeSet, LinkedHashSet (0) | 2022.04.25 |
| [Java] Comparable, Comparator, 정렬 방법 (0) | 2022.04.21 |
| Map 알아보기 (0) | 2022.04.13 |